- Главная
- Программирование на заказ
- Готовые проекты
- Готовые Delphi проекты
- ADO
- АИС, АРМ и АСУ
- Базы данных
- БД библиотек
- Безопасность
- Воинский учет
- Дипломные
- Денежный учет
- Математика
- Учет авто транспорта и комплектующих
- Учет сотрудников
- Товарный учет
- Тесты и электронные учебники
- Инвентаризация
- Магазинный учет
- Образование
- ПК комплектующие
- Складской учет
- Спорт
- Программы учета
- Разное
- Бонусные проекты
- Готовые проекты на C#
- Готовые проекты в C++ Builder
- Проекты на Visual Basic
- Готовые Delphi проекты
- Статьи
- Способы оплаты
- О нас
Транспортная задача на delphi. Метод минимального элемента
Категория:
Решение транспортной задачи на Delphi методом минимального элемента, позволяющей решать задачи оптимизации плана перевозок, по математическим методам программирования.
Название:
Транспортная задача. Метод минимального элемента
Ключевые слова:
решение транспортной задачи в delphi, минимальный элемент в делфи
Код продукта:
35
Язык интерфейса:
- Русский
Платформа:
- Windows
Среда разработки:
- Delphi 7
Описание:
- Имеется
Программа:
Стоимость:
1200.00 руб.
Комплектация:
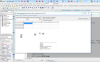
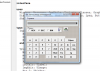
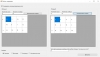
Проект в делфи, скомпилированная программа и пояснительная записка с блок-схемой для написания работы
Краткое описание сущности задачи
В экономике помимо соотношений затрат, выпуска, спроса, предложения и т.п., часто возникает необходимость выбора одного из возможных вариантов функционирования экономической системы. Экономически оправдано в таких условиях, поставить вопрос о выборе наилучшего варианта, который задается в виде критерия - цели. В количественном выражении критерий представляет собой функциональную зависимость от переменных показателей, в дальнейшем будем ее называть целевой функцией. Наилучший вариант в таком случае соответствует наибольшему (экстремальному, оптимальному или наименьшему) значению функции. В экономических задачах такого рода, в основном имеется ограниченная область переменных параметров и, следовательно, оптимальное значение целевой функции нужно найти на ограниченном множестве. Область исследования, заключающаяся в нахождении алгоритмов решения подобных задач, образует направление, которое называется математическим программированием.
В связи с возрастающими требованиями и усложнению задач возникает необходимость разработки специальных методов их решения путем математического программирования.
Распределительные задачи связаны с распределением ресурсов по работам, которые необходимо выполнить. Задачи этого класса возникают тогда, когда имеющихся в наличии ресурсов не хватает для выполнения каждой работы наиболее эффективным образом. Поэтому целью решения задачи, является отыскания такого распределения ресурсов по работам, при котором либо минимизируются общие затраты, связанные с выполнением работ, либо максимизируется получаемый в результате общий доход.

Другие проекты этой группы:
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Комментарии
kandik27
пн, 11/05/2015 - 18:28
kandik27
пн, 11/05/2015 - 18:47
Спасибо нашел решение!